5 Improving Performance
5.1 PARAMETER TUNING
Hyperparameters are model parameters that are specified before training a model – i.e., parameters that are different from model parameters – or weights that an AI/ML model learns during model training.
For many machine learning problems, finding the best hyperparameters is an iterative and potentially time-intensive process called “hyperparameter optimization.
Hyperparameters directly impact the performance of a trained machine-learning model. Choosing the right hyperparameters can dramatically improve prediction accuracy. However, they can be challenging to optimize because there is often a large combination of possible hyperparameter values.
Tuning a machine learning model is an iterative process. Data scientists typically run numerous experiments to train and evaluate models, trying out different features, different loss functions, different AI/ML models, and adjusting model parameters and hyperparameters. Examples of steps involved in tuning and training a machine learning model include feature engineering, loss function formulation, model testing and selection, regularization, and selection of hyperparameters Krishnan (2022).
Let’s assume that you now have a shortlist of promising models. It would help if you now fine-tuned them. Let’s look at a few ways you can do that.
Once we have retrieved optimum values of individual model parameters, we can use grid search to obtain a combination of hyperparameter (The parameters are also known as hyperparameters) values of a model that can give us the highest accuracy.
Grid Search evaluates all possible combinations of the parameter values.
Grid Search is exhaustive and uses brute force to evaluate the most accurate values. Therefore it is a computationally intensive task.
house<-read.csv("data/house_clean.csv")
#house<-read.csv("https://raw.githubusercontent.com/abernal30/ml_book/main/housing.csv")
set.seed (26)
dim<-dim(house)
train_sample<-sample(dim[1],dim[1]*.8)
house_train <- house[train_sample, ]
house_test <- house[-train_sample, ]
library(caret)
set.seed (26)
fitControl <- trainControl(method = "cv",
number = 10)
gbmFit <- train(SalePrice ~ ., data = house_train,
method = "gbm",
trControl = fitControl,
verbose = FALSE)
gbmFit
#> Stochastic Gradient Boosting
#>
#> 467 samples
#> 51 predictor
#>
#> No pre-processing
#> Resampling: Cross-Validated (10 fold)
#> Summary of sample sizes: 420, 421, 421, 419, 420, 421, ...
#> Resampling results across tuning parameters:
#>
#> interaction.depth n.trees RMSE Rsquared MAE
#> 1 50 47239.17 0.7444321 30600.93
#> 1 100 46147.22 0.7537532 29225.96
#> 1 150 45741.85 0.7555015 28969.01
#> 2 50 45232.87 0.7570658 28665.82
#> 2 100 44866.17 0.7601488 27908.81
#> 2 150 45748.88 0.7554831 27734.49
#> 3 50 44032.44 0.7708265 27661.85
#> 3 100 43706.40 0.7775313 26762.67
#> 3 150 44620.73 0.7733739 27046.71
#>
#> Tuning parameter 'shrinkage' was held constant at a value of 0.1
#>
#> Tuning parameter 'n.minobsinnode' was held constant at a value of 10
#> RMSE was used to select the optimal model using the smallest value.
#> The final values used for the model were n.trees = 100, interaction.depth =
#> 3, shrinkage = 0.1 and n.minobsinnode = 10.
min(gbmFit$results[,"RMSE"])
#> [1] 43706.4
seq(0.08,0.2,.01)
#> [1] 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19 0.20
set.seed (26)
fitControl <- trainControl(method = "cv",
number = 10)
gbmGrid <- expand.grid(interaction.depth = 3,
n.trees = 100,
shrinkage = seq(0.08,0.2,.01),
n.minobsinnode = c(10,20,30))
nrow(gbmGrid)
#> [1] 39
gbmFit2 <- train(SalePrice ~ ., data = house_train,
method = "gbm",
trControl = fitControl,
verbose = FALSE,
## Now specify the exact models
## to evaluate:
tuneGrid = gbmGrid)
gbmFit2
#> Stochastic Gradient Boosting
#>
#> 467 samples
#> 51 predictor
#>
#> No pre-processing
#> Resampling: Cross-Validated (10 fold)
#> Summary of sample sizes: 420, 421, 421, 419, 420, 421, ...
#> Resampling results across tuning parameters:
#>
#> shrinkage n.minobsinnode RMSE Rsquared MAE
#> 0.08 10 43689.38 0.7757923 26414.49
#> 0.08 20 43439.41 0.7762678 26253.74
#> 0.08 30 43718.02 0.7740018 27043.45
#> 0.09 10 44482.73 0.7657377 26932.51
#> 0.09 20 44471.18 0.7694100 26930.13
#> 0.09 30 42765.74 0.7850388 26107.17
#> 0.10 10 45797.81 0.7565011 27752.53
#> 0.10 20 43305.74 0.7752004 26133.99
#> 0.10 30 44014.90 0.7733803 27155.20
#> 0.11 10 44489.95 0.7656922 26866.05
#> 0.11 20 44102.22 0.7772802 26763.98
#> 0.11 30 43173.50 0.7852119 26475.20
#> 0.12 10 45685.92 0.7560192 27278.29
#> 0.12 20 43837.29 0.7733656 26780.05
#> 0.12 30 43632.73 0.7731039 27097.95
#> 0.13 10 45015.04 0.7633598 27339.32
#> 0.13 20 44378.70 0.7733293 26922.59
#> 0.13 30 43729.28 0.7738287 26848.09
#> 0.14 10 45847.55 0.7616066 26985.59
#> 0.14 20 43476.83 0.7753577 27154.57
#> 0.14 30 44204.43 0.7733527 27236.38
#> 0.15 10 46597.58 0.7505296 27959.85
#> 0.15 20 45481.20 0.7606624 27931.86
#> 0.15 30 44495.46 0.7689698 27904.48
#> 0.16 10 46312.23 0.7551459 28093.47
#> 0.16 20 44609.52 0.7720711 26788.57
#> 0.16 30 44293.15 0.7709916 27231.55
#> 0.17 10 47092.71 0.7503482 27909.55
#> 0.17 20 45266.73 0.7597926 27838.44
#> 0.17 30 44495.99 0.7682215 27612.17
#> 0.18 10 46187.08 0.7560767 27455.96
#> 0.18 20 45563.69 0.7615617 28022.82
#> 0.18 30 44019.18 0.7697064 28476.80
#> 0.19 10 49851.20 0.7284168 29410.44
#> 0.19 20 46902.27 0.7505154 28841.09
#> 0.19 30 44854.58 0.7651957 28353.89
#> 0.20 10 48231.76 0.7329092 29188.07
#> 0.20 20 44947.66 0.7651168 27865.51
#> 0.20 30 44618.00 0.7586902 27987.05
#>
#> Tuning parameter 'n.trees' was held constant at a value of 100
#> Tuning
#> parameter 'interaction.depth' was held constant at a value of 3
#> RMSE was used to select the optimal model using the smallest value.
#> The final values used for the model were n.trees = 100, interaction.depth =
#> 3, shrinkage = 0.09 and n.minobsinnode = 30.
trellis.par.set(caretTheme())
plot(gbmFit2) 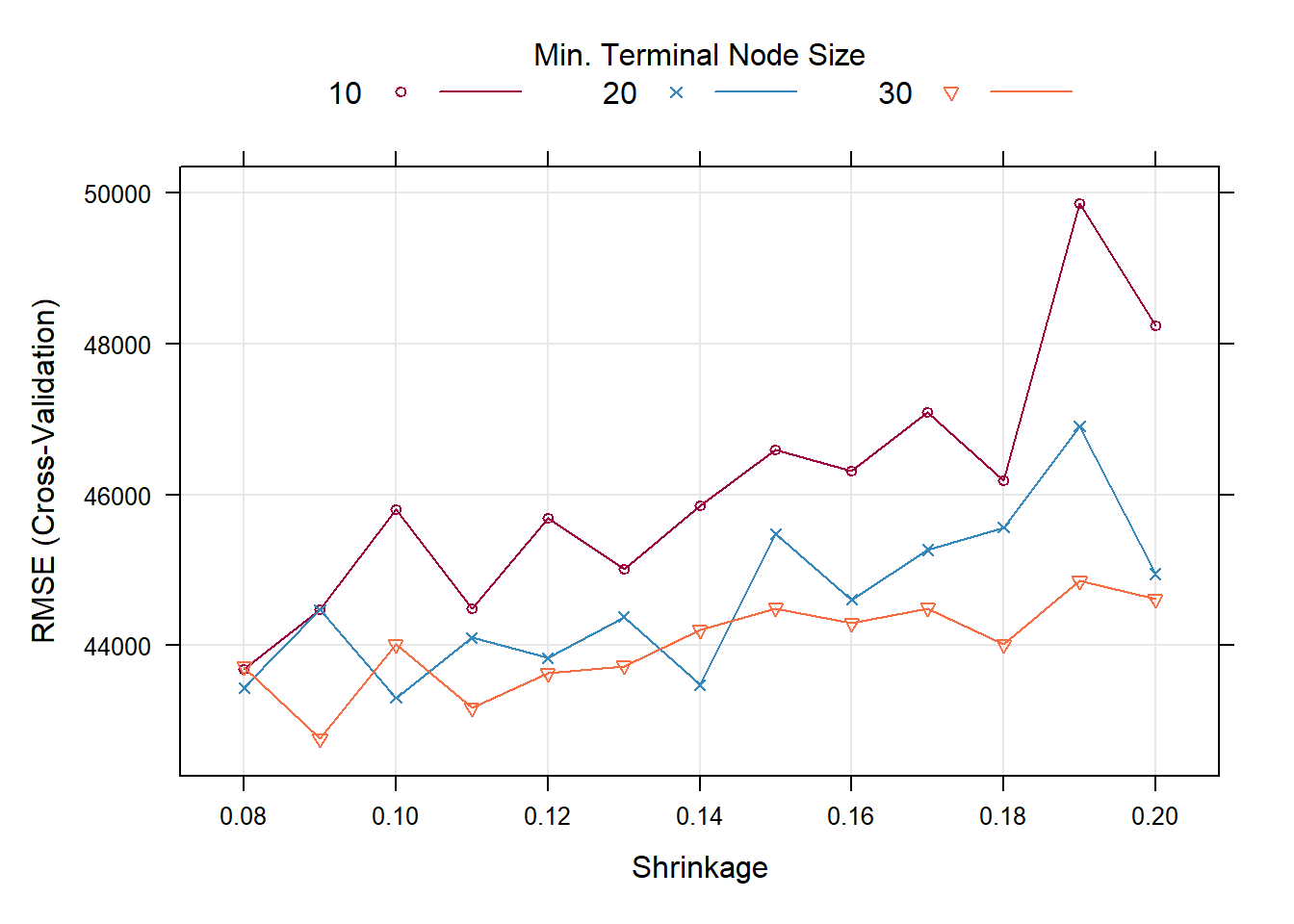
gbmFit2$bestTune
#> n.trees interaction.depth shrinkage n.minobsinnode
#> 6 100 3 0.09 30
set.seed (26)
fitControl <- trainControl(method = "cv",
number = 10)
gbmGrid <- expand.grid(interaction.depth = 3,
n.trees = 100,
shrinkage = 0.09,
n.minobsinnode = 30)
gbmFit1 <- train(SalePrice ~ ., data = house_train,
method = "gbm",
trControl = fitControl,
verbose = FALSE,tuneGrid = gbmGrid)
gbmFit1
#> Stochastic Gradient Boosting
#>
#> 467 samples
#> 51 predictor
#>
#> No pre-processing
#> Resampling: Cross-Validated (10 fold)
#> Summary of sample sizes: 420, 421, 421, 419, 420, 421, ...
#> Resampling results:
#>
#> RMSE Rsquared MAE
#> 43538.88 0.7755887 27051.03
#>
#> Tuning parameter 'n.trees' was held constant at a value of 100
#> Tuning
#>
#> Tuning parameter 'shrinkage' was held constant at a value of 0.09
#>
#> Tuning parameter 'n.minobsinnode' was held constant at a value of 305.2 Analyze the Best Models and Their Errors
set.seed (26)
lmFit <- train(SalePrice ~ ., data = house_train,
method = "lm",
trControl = fitControl)
lmFit
#> Linear Regression
#>
#> 467 samples
#> 51 predictor
#>
#> No pre-processing
#> Resampling: Cross-Validated (10 fold)
#> Summary of sample sizes: 420, 421, 421, 419, 420, 421, ...
#> Resampling results:
#>
#> RMSE Rsquared MAE
#> 53829.9 0.7130432 32074.47
#>
#> Tuning parameter 'intercept' was held constant at a value of TRUE
k2<-10
set.seed (26)
fitControl3 <- trainControl(method = "cv",
number = k2)
step <- train(SalePrice ~ ., data = house_train,
method = "lmStepAIC",
trControl = fitControl3, trace=F)
step
#> Linear Regression with Stepwise Selection
#>
#> 467 samples
#> 51 predictor
#>
#> No pre-processing
#> Resampling: Cross-Validated (10 fold)
#> Summary of sample sizes: 420, 421, 421, 419, 420, 421, ...
#> Resampling results:
#>
#> RMSE Rsquared MAE
#> 53183.1 0.7218324 31441.74
resamps <- resamples(list(GBM = gbmFit1,
lm= lmFit,
step = step))
summary(resamps)
#>
#> Call:
#> summary.resamples(object = resamps)
#>
#> Models: GBM, lm, step
#> Number of resamples: 10
#>
#> MAE
#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> GBM 16916.01 22683.84 26802.82 27051.03 33250.31 34700.58 0
#> lm 24099.97 27569.17 32581.94 32074.47 33796.23 46936.58 0
#> step 23457.60 27519.35 31131.39 31441.74 33246.95 47069.12 0
#>
#> RMSE
#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> GBM 21042.28 29863.83 42580.60 43538.88 53434.67 68983.63 0
#> lm 29902.95 38797.25 46407.32 53829.90 50676.37 142708.97 0
#> step 29473.14 38261.54 45661.85 53183.10 49510.85 142365.64 0
#>
#> Rsquared
#> Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
#> GBM 0.4466954 0.7499098 0.7749271 0.7755887 0.8692610 0.9222225 0
#> lm 0.1182236 0.7380041 0.7705471 0.7130432 0.7989847 0.8440776 0
#> step 0.1201389 0.7623466 0.7765474 0.7218324 0.7931811 0.8461111 0
theme1 <- trellis.par.get()
theme1$plot.symbol$col = rgb(.2, .2, .2, .4)
theme1$plot.symbol$pch = 16
theme1$plot.line$col = rgb(1, 0, 0, .7)
theme1$plot.line$lwd <- 2
trellis.par.set(theme1)
bwplot(resamps, layout = c(3, 1))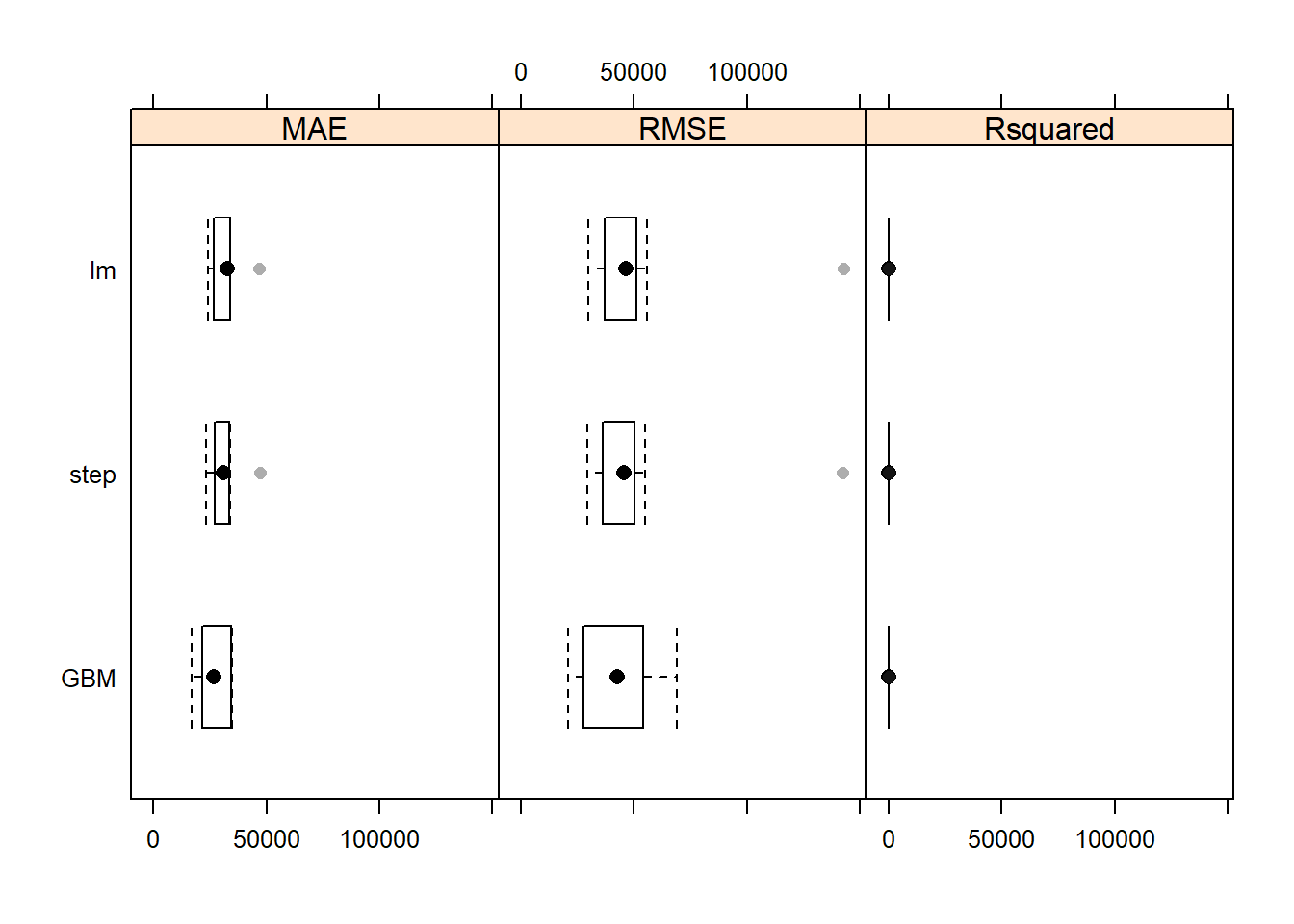 —no
—no5.3 Evaluate Your System on the Test Set
library(gbm)
gbm1 <-gbm(SalePrice ~ ., data = house_train, n.trees = 100, shrinkage = 0.09,
interaction.depth = 3, distribution = "gaussian",bag.fraction = 0.5, train.fraction = 0.5,
n.minobsinnode = 30, cv.folds = 10, keep.data = TRUE,
verbose = FALSE)
best.iter <- gbm.perf(gbm1, method = "cv")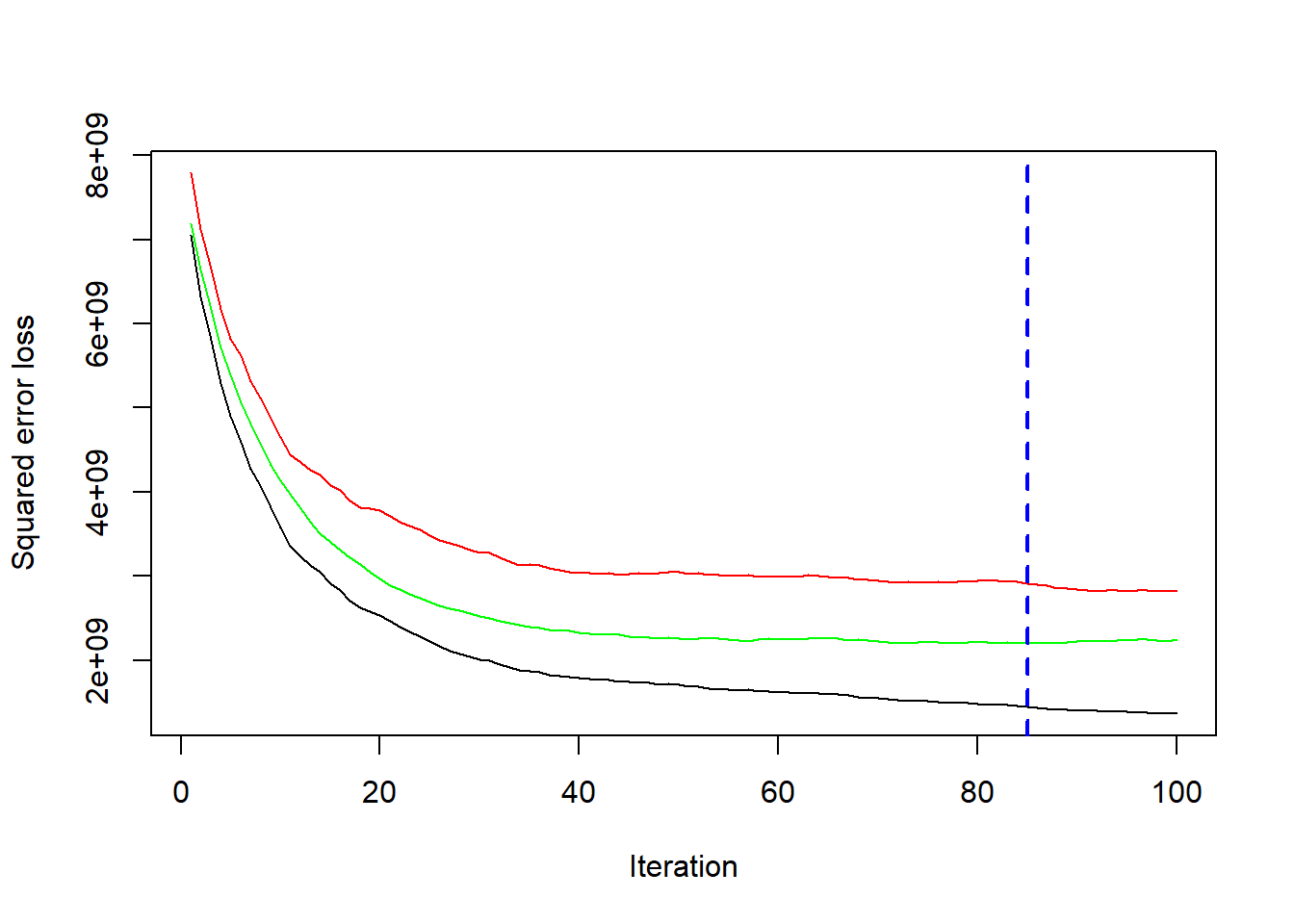
print(best.iter)
#> [1] 85