6 Clustering
Unsupervised learning - Clustering
Clustering is a technique that aims to group similar data points so that the points in the same group have similar features to those in the other groups. The group of similar data points is called a Cluster.
For example, suppose we have the following data frame, with hypothetical data of students ages and grades in course:
set.seed(1100)
x <- round(rnorm(12, 20, 3),0)
y <- round(rnorm(12, 95, 4),0)
y<-ifelse(y>100,100,y)
df<- data.frame(Age=x, Grade=y)
rownames(df)<-paste("Ind",rownames(df))
df
#> Age Grade
#> Ind 1 21 100
#> Ind 2 19 98
#> Ind 3 20 95
#> Ind 4 17 97
#> Ind 5 17 95
#> Ind 6 21 97
#> Ind 7 19 96
#> Ind 8 19 97
#> Ind 9 16 87
#> Ind 10 25 95
#> Ind 11 23 97
#> Ind 12 22 100For a betther undestandng of what is a plot, the following plot shows how each person is similar to other in terms of age and grade.
plot(df[,"Age"], df[,"Grade"], col = "blue", pch = 1, cex = 1.5,ylab="Grade",xlab="Age",ylim=c(88,101),xlim=c(16,26))
text(df[,"Age"] + .3, df[,"Grade"] + 0.9, labels = rownames(df))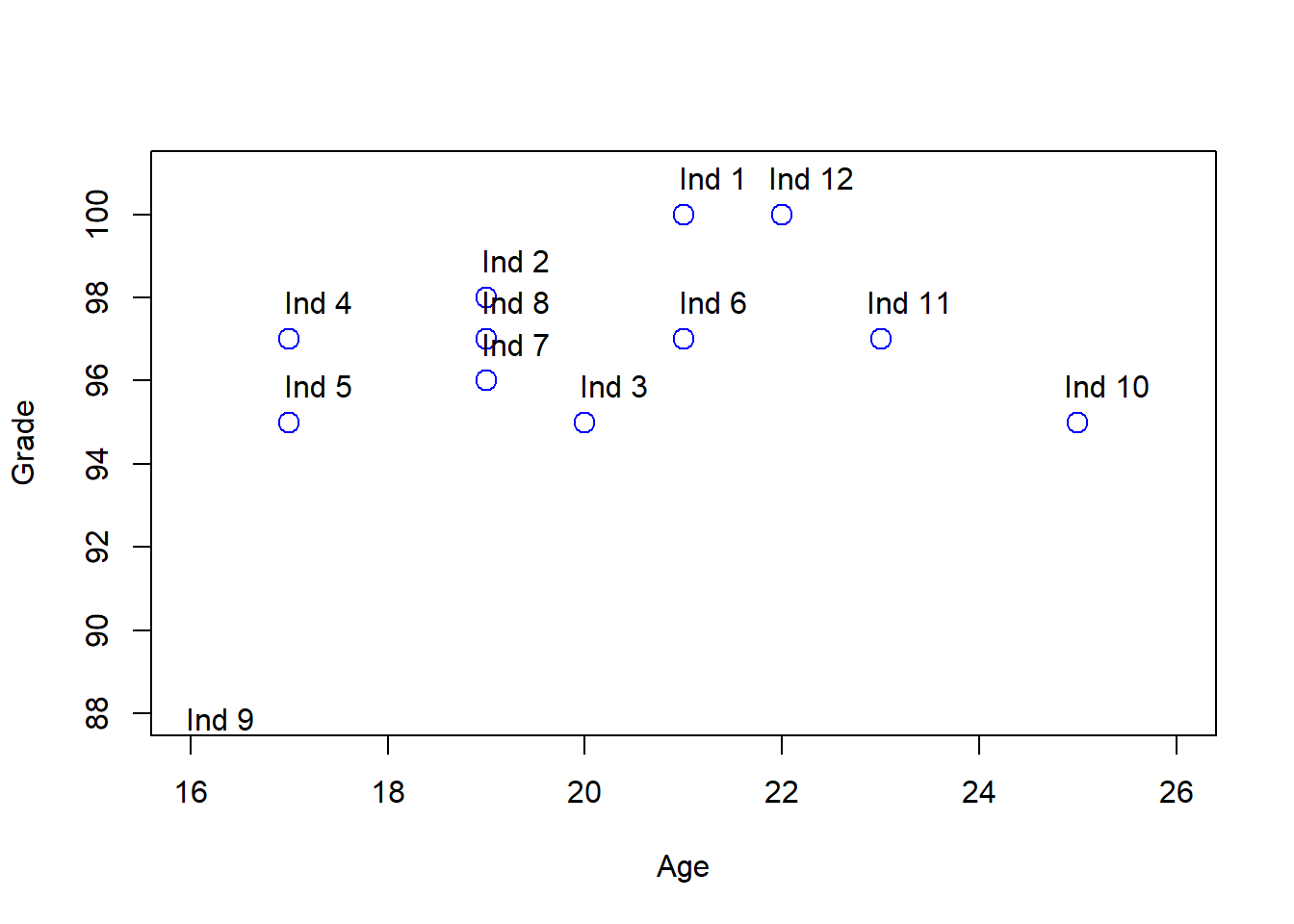
One one to identify if a person or a group of persons are similar in terms of age and grade to other, which is equivalent to say that are in the same cluster, is using the Euclidean Distance (ED):
\[d_{euc}(p,q)= \sqrt{ \sum_{i=1}^{n} (p_{i}-q_{i}})^{2}\]
where \(p_{i}\), \(p_{i}\) are two points in the euclidean space. In our example, are two different persons of the data set. \(n\) is the number of features, in our example are two, age anf grade. For example, the Euclidean Distance for person 1 and 2 is:
sqrt((df["Ind 1","Age"]-df["Ind 2","Age"])^2+(df["Ind 1","Grade"]-df["Ind 2","Grade"])^2)
#> [1] 2.828427The lower (higher) the ED between two persons, the more similars (different) they are, and is porbably that are grouped (not grouped) in the same cluster.
To estimate the Euclidean Distance for all the persons in the data set, we use the funciton “get_dist”, from the library “factoextra”:
library(factoextra) #
distance<-get_dist(df, method = "euclidean")
distance
#> Ind 1 Ind 2 Ind 3 Ind 4 Ind 5 Ind 6 Ind 7
#> Ind 2 2.828427
#> Ind 3 5.099020 3.162278
#> Ind 4 5.000000 2.236068 3.605551
#> Ind 5 6.403124 3.605551 3.000000 2.000000
#> Ind 6 3.000000 2.236068 2.236068 4.000000 4.472136
#> Ind 7 4.472136 2.000000 1.414214 2.236068 2.236068 2.236068
#> Ind 8 3.605551 1.000000 2.236068 2.000000 2.828427 2.000000 1.000000
#> Ind 9 13.928388 11.401754 8.944272 10.049876 8.062258 11.180340 9.486833
#> Ind 10 6.403124 6.708204 5.000000 8.246211 8.000000 4.472136 6.082763
#> Ind 11 3.605551 4.123106 3.605551 6.000000 6.324555 2.000000 4.123106
#> Ind 12 1.000000 3.605551 5.385165 5.830952 7.071068 3.162278 5.000000
#> Ind 8 Ind 9 Ind 10 Ind 11
#> Ind 2
#> Ind 3
#> Ind 4
#> Ind 5
#> Ind 6
#> Ind 7
#> Ind 8
#> Ind 9 10.440307
#> Ind 10 6.324555 12.041595
#> Ind 11 4.000000 12.206556 2.828427
#> Ind 12 4.242641 14.317821 5.830952 3.162278As we see in the output, the result shows the ED between each person. Is important to notice that the output is not a data frame, is a “dist” object:
class(distance)
#> [1] "dist"The previous outpt is not giving us infromation about how people are grouped in clusters, but the following plot does, using the function “fviz_dist”, wich has as first argument the “dist” object we made in the last “chunk”:
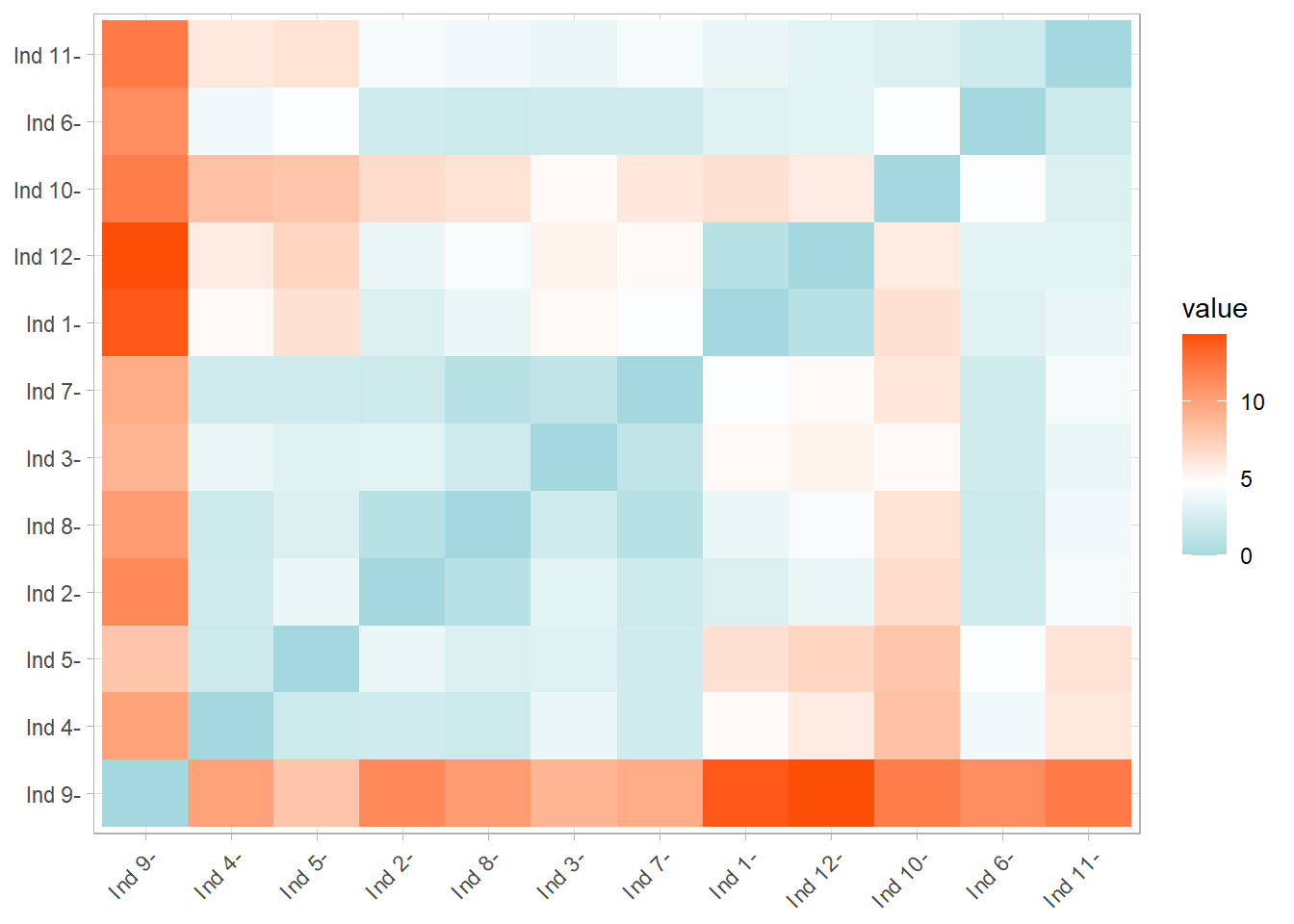
In the previous plot, the red color squares are persons with a higher ED and the blue ones lower ones.
In terms of the scatter plot we made before, if we take the individual pairs that has a ED less than 2, for example, we get the following results:
plot(df[,"Age"], df[,"Grade"], col = "blue", pch = 1, cex = 1.5,ylab="Grade",xlab="Age",ylim=c(86,101),xlim=c(16,26))
text(df[,"Age"] + .3, df[,"Grade"] + 0.6, labels = rownames(df))
points(df[ind[1, ],"Age"], df[ind[1, ],"Grade"], col = "orange", pch = 19, cex = 2)
points(df[ind[2, ],"Age"], df[ind[2, ],"Grade"], col = "red", pch = 19, cex = 2)
points(df[ind[3, ],"Age"], df[ind[3, ],"Grade"], col = "red", pch = 19, cex = 2)
points(df[ind[4, ],"Age"], df[ind[4, ],"Grade"], col = "red", pch = 19, cex = 2)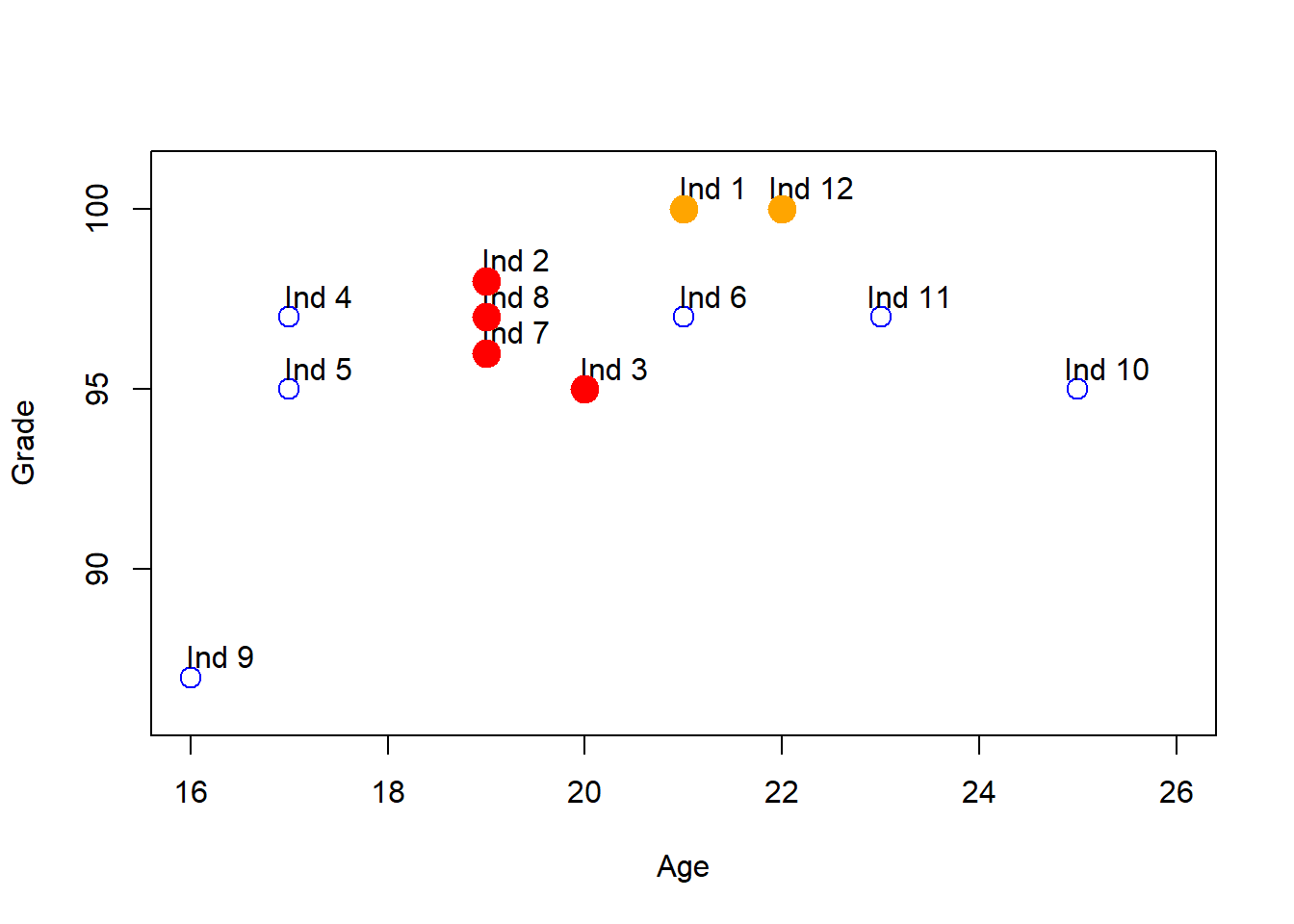
#segments(x0 = 19, y0 = 96,x1=20,y1=95) We see that the red dots are kind of grouped between them, and also the yellow ones. In this sense, we could say that the individuals in red dots could be a cluster, and the individuals in yellow other cluster. We could repeat the procees for the no-color individuales, but for the moment we waned to explian how clusters are formed.
6.1 Agglomerative hierarchical clustering
As we prove in the last method, we need a partition to define the similarity beetween two individuals, to be in th sale cluster. Hierarchical clustering algorithms doesn´t need a predefined partition to generate the clusters.
First, using a particular proximity measure a dissimilarity matrix is constructed and all the data points are visually represented at the bottom of the dendrogram. The closest sets of clusters are merged at each level and then the dissimilarity matrix is updated correspondingly. This process of agglomerative merging is carried on until the final maximal cluster (that contains all the data objects in a single cluster) is obtained. This would represent the apex of our dendrogram and mark the completion of the merging process. We will now discuss the different kinds of proximity measures which can be used in agglomerative hierarchical clustering. Subsequently, we will also provide a complete version of the agglomerative hierarchical clustering algorithm in
The most popular agglomerative clustering methods are single link and complete link clusterings. In single link clustering [36, 46], the similarity of two clusters is the similarity between their most similar (nearest neighbor) members. This method intuitively gives more importance to the regions where clusters are closest, neglecting the overall structure of the cluster. Hence, this method falls under the category of a local similarity-based clustering method. Because of its local behavior, single linkage is capable of effectively clustering nonelliptical, elongated shaped groups of data objects. However, one of the main drawbacks of this method is its sensitivity to noise and outliers in the data.
Complete link clustering [27] measures the similarity of two clusters as the similarity of their most dissimilar members. This is equivalent to choosing the cluster pair whose merge has the smallest diameter. As this method takes the cluster structure into consideration it is nonlocal in behavior and generally obtains compact shaped clusters. However, similar to single link clustering, this method is also sensitive to outliers. Both single link and complete link clustering have their graph-theoretic interpretations [16], where the clusters obtained after single link clustering would correspond to the connected components of a graph and those obtained through complete link would correspond to the maximal cliques of the graph.
The Lance and Williams recurrence formula gives the distance between a group k and a group (ij) formed by the fusion of two groups (i and j) as :
\[ d_{k(ij)}= \alpha\ d_{ki}+\beta\ d_{ij}+\gamma\ |d_{ki}-d_{kj}|, \]
where \(d_{ij}\) is s the distance between groups i and j. Lance and Williams used the formula to define a new ‘flexible’ scheme, with parameter values αi + αj + β = 1, αi = αj, β < 1, γ = 0. By allowing β to vary, clustering schemes with various characteristics can be obtained. They suggest small negative values for β, such as −0.25, although Scheibler and Schneider (1985) suggest −0.50 (Brian S. Everitt 2011).
hClustering <- hclust(distance object,method) method=c(ward.D”, “ward.D2”, “single”, “complete”, “average”, “mcquitty” , “median” or “centroid” )
plot(hClustering object)
hClustering <- hclust(distance ,method="single") # cuidado por que le pusimos distance también al de teens
plot(hClustering)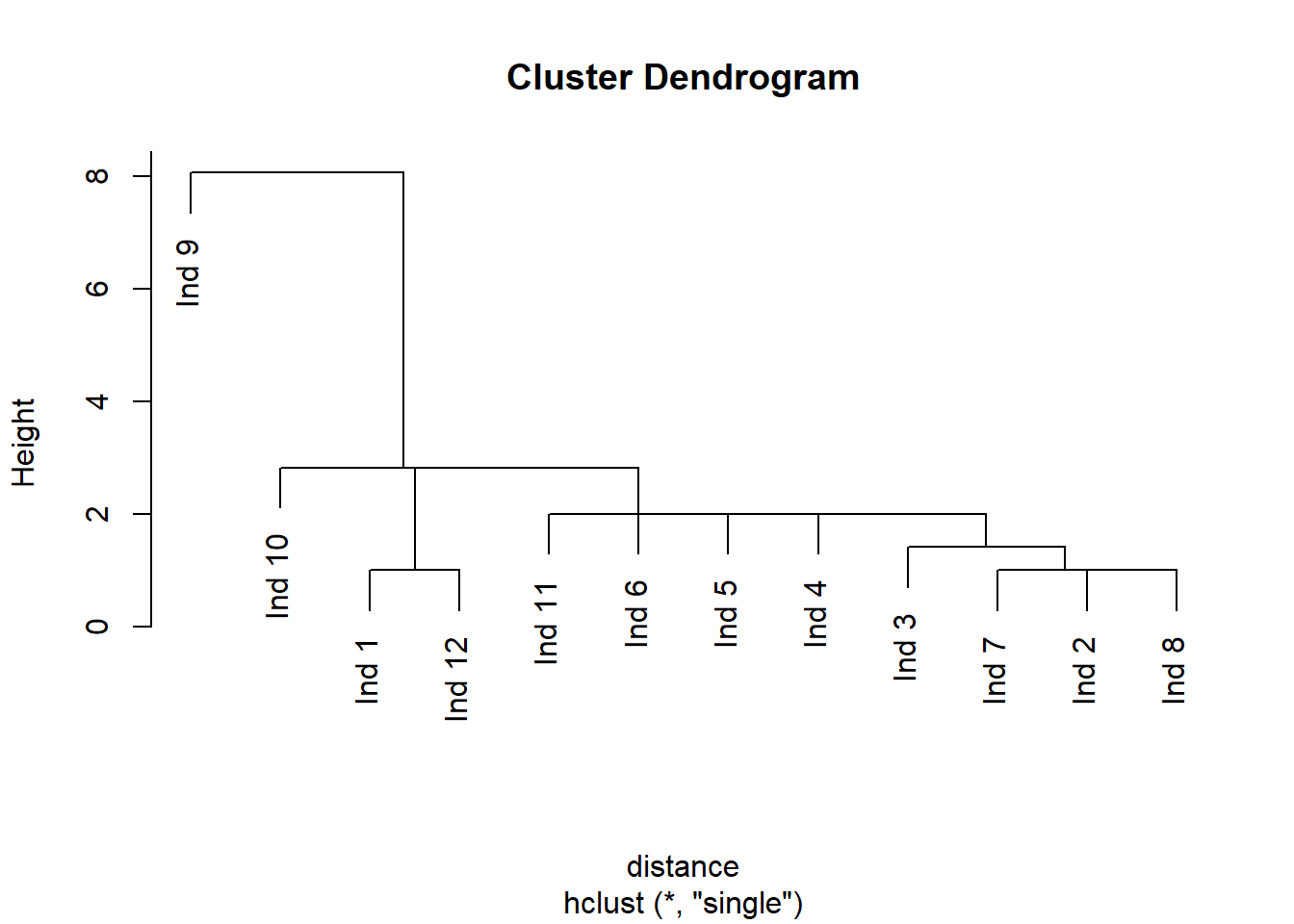
This chart can be used to visually inspect the number of clusters that would be created for a selected distance threshold . The number of vertical lines a hypothetical straight, horizontal line will pass through is the number of clusters created for that distance threshold value. All data points (leaves) from that branch would be labeled as that cluster that the horizontal line passed through.
members of each cluster memb <-cutree(hClustering object, k = )
k= número de clusters que se desean
h= cut number of the dendrogram
6.2 K-Means Clustering
K-means clustering is the most commonly used unsupervised machine learning algorithm for partitioning a given data set into a set of k groups (i.e. k clusters), where k represents the number of groups pre-specified by the analyst. It classifies objects in multiple groups (i.e., clusters), such that objects within the same cluster are as similar as possible (i.e., high intra-class similarity), whereas objects from different clusters are as dissimilar as possible (i.e., low inter-class similarity). In k-means clustering, each cluster is represented by its center (i.e, centroid) which corresponds to the mean of points assigned to the cluster.
The Basic Idea
The basic idea behind k-means clustering consists of defining clusters so that the total intra-cluster variation (known as total within-cluster variation) is minimized. There are several k-means algorithms available. The standard algorithm is the Hartigan-Wong algorithm (1979), which defines the total within-cluster variation as the sum of squared distances Euclidean distances between items and the corresponding centroid:
\[ W(C_{k})=\sum_{x_{i}\in C_{k}}(x_{i}- \mu_{k})^2\]
\(x_{i}\) is a data point belonging to the cluster Ck.
_{k} is the mean value of the points assigned to the cluster Ck
Each observation (xi) is assigned to a given cluster such that the sum of squares (SS) distance of the observation to their assigned cluster centers (μk) is minimized.
We define the total within-cluster variation as follows: \[ tot.withiness=\sum_{k=1}^k W(C_{k})=\sum_{k=1}^k \sum_{x_{i}\in C_{k}}(x_{i}- \mu_{k})^2\]
The total within-cluster sum of square measures the compactness (i.e goodness) of the clustering and we want it to be as small as possible.
kmeans(df object, centers = ) centers is number of clusters
nstart, Select randomly k objects from the data set as the initial cluster centers or means
set.seed(1234)
# regresamos a df con dos variables
teens<-read.csv("https://raw.githubusercontent.com/abernal30/ml_book/main/teens_clean.csv")
set.seed(200)
teens_na<-na.omit(teens)
#dim arroja el npumero de renglones y columas de un data frame
dim<-dim(teens_na)
# genera números del 1 al 27,276(dim[1]) pero solo arrojame 1,000.
samp<-sample(dim[1],10000)
# Del objeto teens_na, toma solo las observaciones que hay en samp
teens_2<-teens_na[samp,]
teens_2[,"gender"]<-ifelse(teens_2[,"gender"]=="F",1,0)
km<-kmeans(teens_2, centers = 3) # centers es el número de clustersfviz_cluster(kmenas object, data =, stand=F)
ylim=c(90,101),xlim=c(17,27)
fviz_cluster(km, data = teens_2 , stand=F)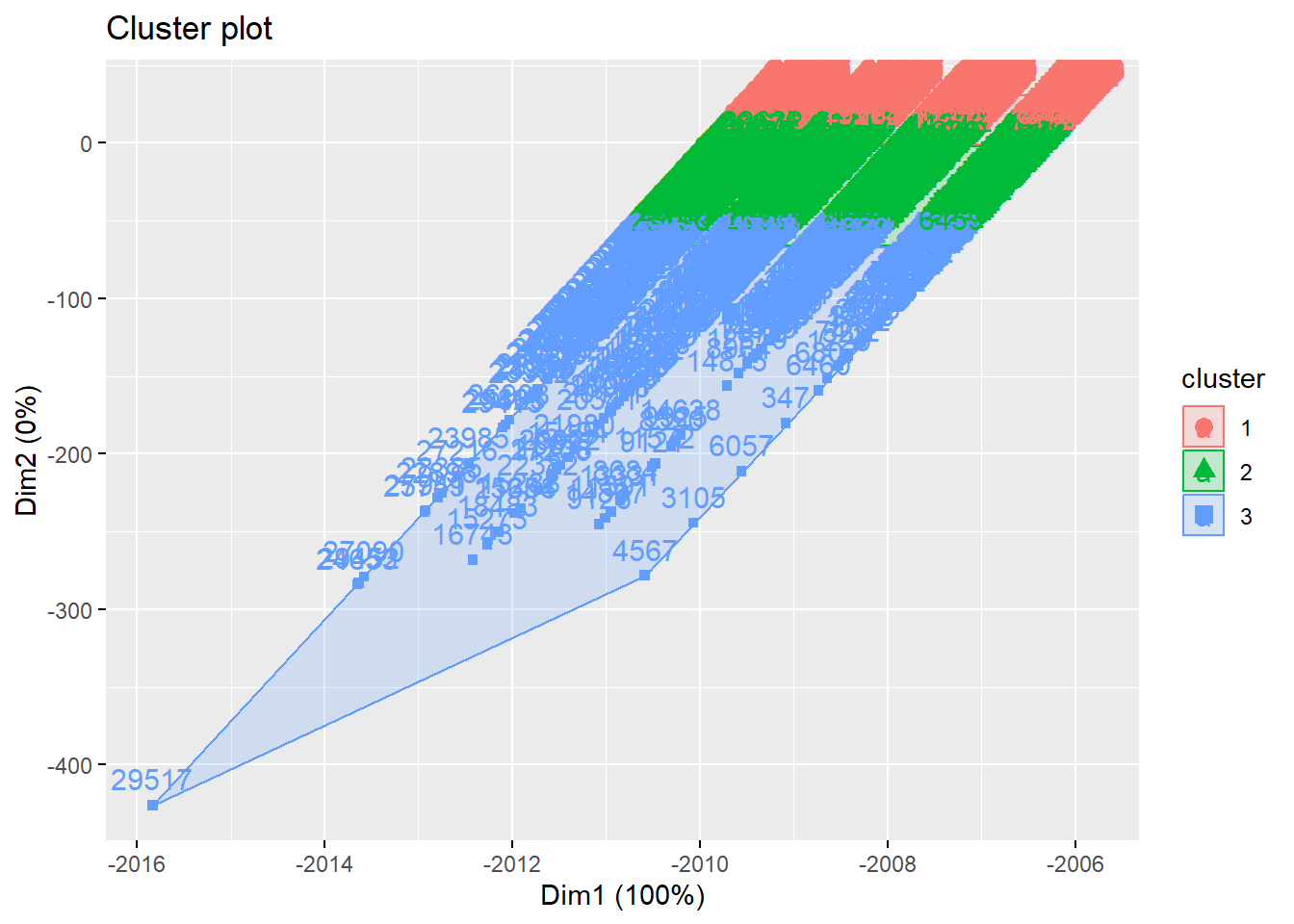
set.seed(123)
fviz_nbclust(teens_2 , kmeans, method = "wss")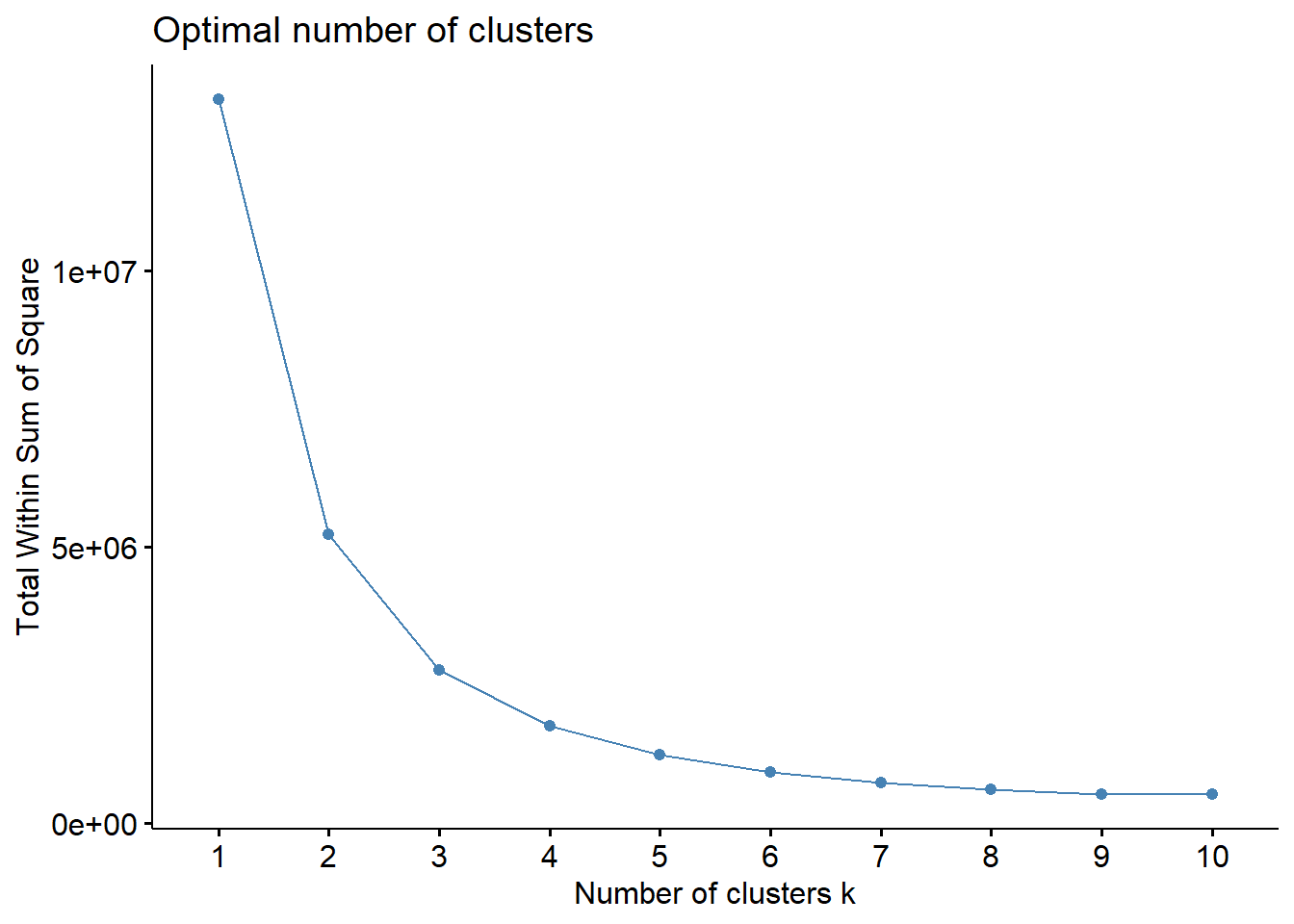
Elbow Method
Recall that, the basic idea behind cluster partitioning methods, such as k-means clustering, is to define clusters such that the total intra-cluster variation (known as total within-cluster variation or total within-cluster sum of square) is minimized:
set.seed(123)
fviz_nbclust(teens_2, kmeans, method = "wss")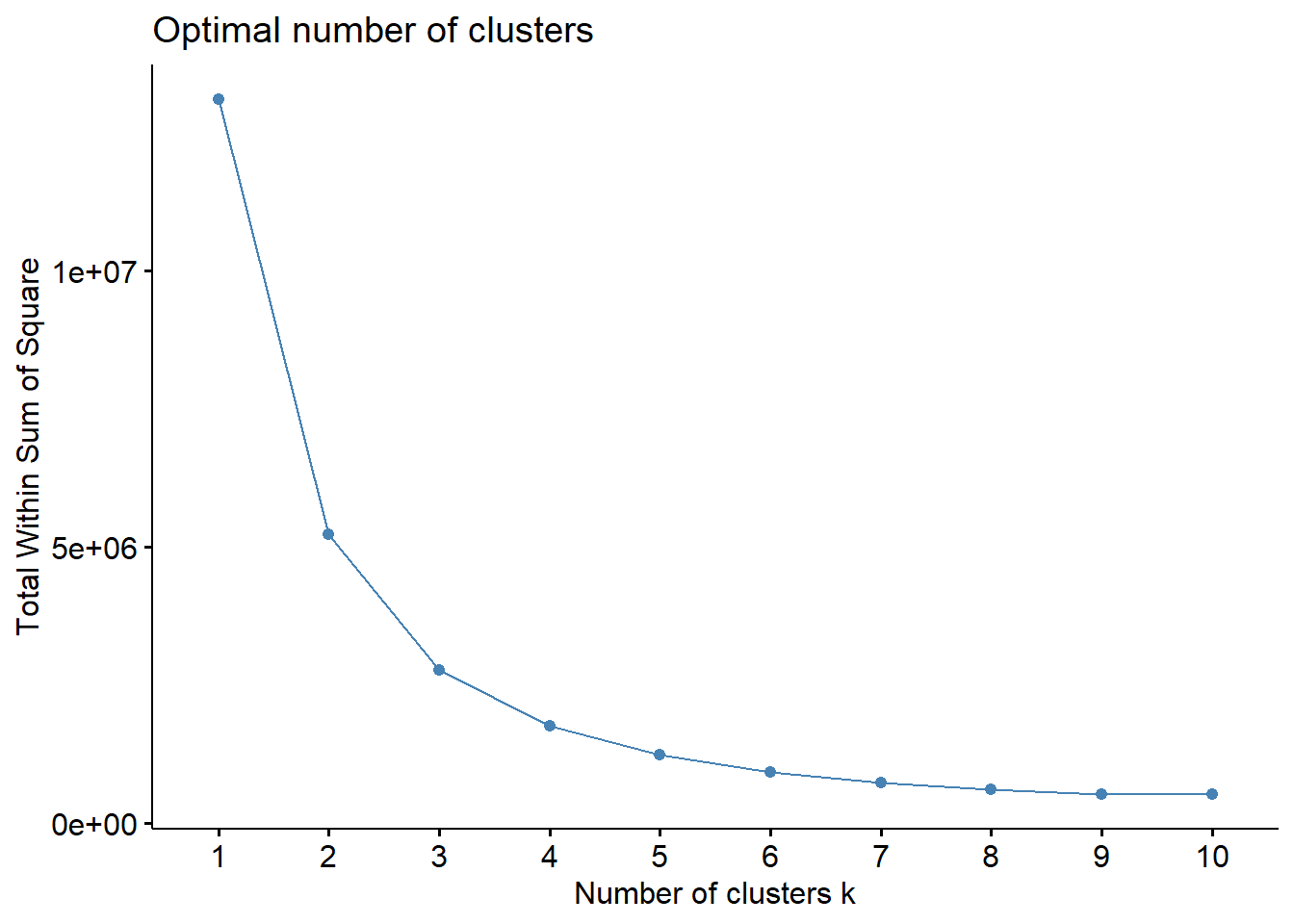
Average Silhouette Method
In short, the average silhouette approach measures the quality of a clustering. That is, it determines how well each object lies within its cluster. A high average silhouette width indicates a good clustering. The average silhouette method computes the average silhouette of observations for different values of k. The optimal number of clusters k is the one that maximizes the average silhouette over a range of possible values for k.2
We can use the silhouette function in the cluster package to compuate the average silhouette width. The following code computes this approach for 1-15 clusters. The results show that 2 clusters maximize the average silhouette values with 4 clusters coming in as second optimal number of clusters.
set.seed(123)
fviz_nbclust(df, kmeans, method = "silhouette")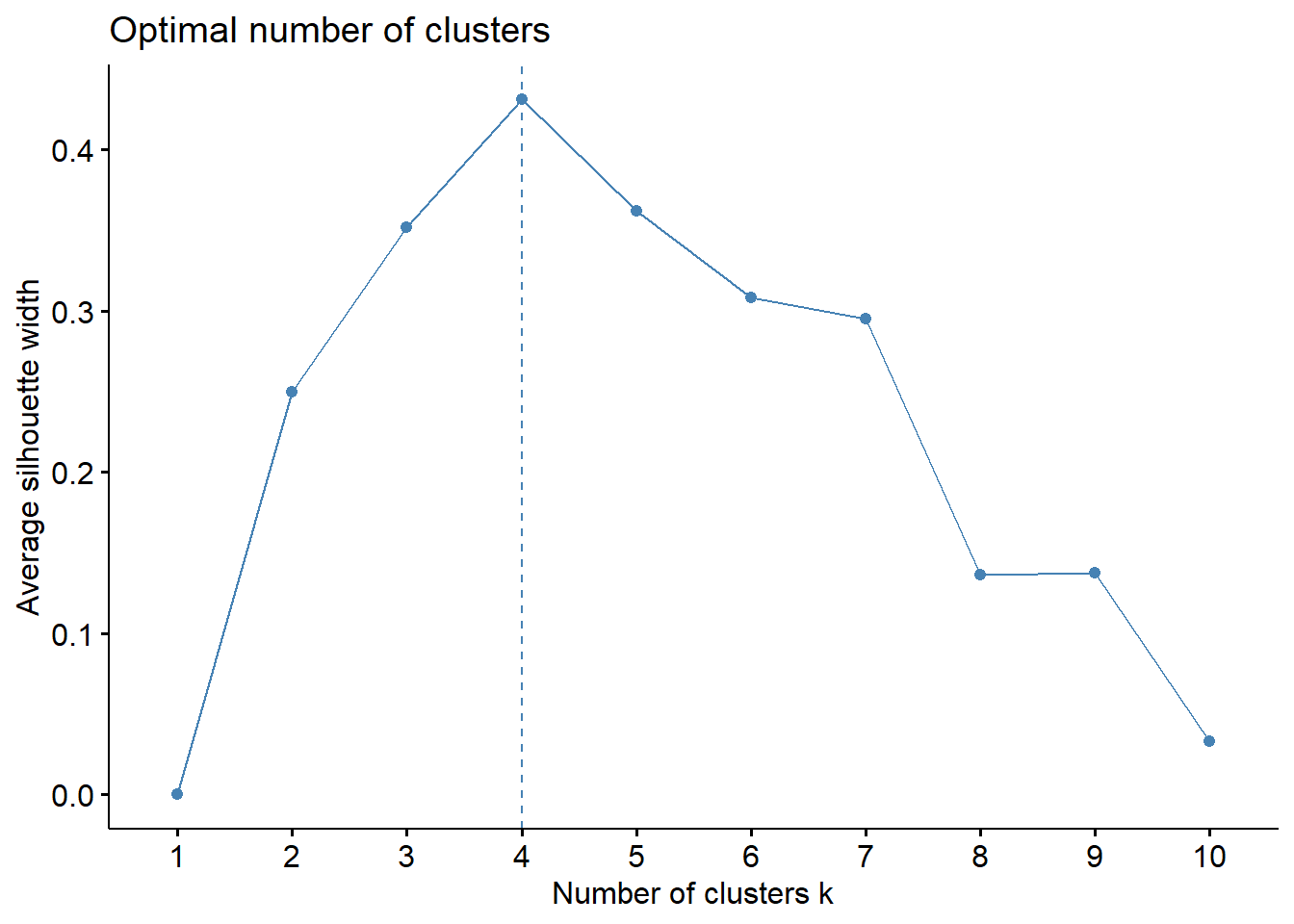
6.3 Cluster intuition
We do the cluster intuition only for the k-means, but it could apply for other methods, such as hierarchical clustering.
teens_scale<-as.data.frame(lapply(teens_2[,2:41], scale))
summary(teens_scale)
#> gender age friends basketball
#> Min. :-2.0727 Min. :-3.306980 Min. :-0.8569 Min. :-0.3403
#> 1st Qu.: 0.4824 1st Qu.:-0.829209 1st Qu.:-0.7455 1st Qu.:-0.3403
#> Median : 0.4824 Median :-0.007369 Median :-0.2720 Median :-0.3403
#> Mean : 0.0000 Mean : 0.000000 Mean : 0.0000 Mean : 0.0000
#> 3rd Qu.: 0.4824 3rd Qu.: 0.843353 3rd Qu.: 0.3687 3rd Qu.:-0.3403
#> Max. : 0.4824 Max. : 2.396008 Max. :11.8721 Max. :15.4215
#> football soccer softball volleyball
#> Min. :-0.3696 Min. :-0.2452 Min. :-0.2245 Min. :-0.2259
#> 1st Qu.:-0.3696 1st Qu.:-0.2452 1st Qu.:-0.2245 1st Qu.:-0.2259
#> Median :-0.3696 Median :-0.2452 Median :-0.2245 Median :-0.2259
#> Mean : 0.0000 Mean : 0.0000 Mean : 0.0000 Mean : 0.0000
#> 3rd Qu.:-0.3696 3rd Qu.:-0.2452 3rd Qu.:-0.2245 3rd Qu.:-0.2259
#> Max. :13.8005 Max. :28.5005 Max. :16.2346 Max. :17.2642
#> swimming cheerleading baseball tennis
#> Min. :-0.2829 Min. :-0.211 Min. :-0.193 Min. :-0.1663
#> 1st Qu.:-0.2829 1st Qu.:-0.211 1st Qu.:-0.193 1st Qu.:-0.1663
#> Median :-0.2829 Median :-0.211 Median :-0.193 Median :-0.1663
#> Mean : 0.0000 Mean : 0.000 Mean : 0.000 Mean : 0.0000
#> 3rd Qu.:-0.2829 3rd Qu.:-0.211 3rd Qu.:-0.193 3rd Qu.:-0.1663
#> Max. :15.8853 Max. :16.050 Max. :25.838 Max. :22.9600
#> sports cute sex sexy
#> Min. :-0.2982 Min. :-0.4074 Min. :-0.2128 Min. :-0.2697
#> 1st Qu.:-0.2982 1st Qu.:-0.4074 1st Qu.:-0.2128 1st Qu.:-0.2697
#> Median :-0.2982 Median :-0.4074 Median :-0.2128 Median :-0.2697
#> Mean : 0.0000 Mean : 0.0000 Mean : 0.0000 Mean : 0.0000
#> 3rd Qu.:-0.2982 3rd Qu.:-0.4074 3rd Qu.:-0.2128 3rd Qu.:-0.2697
#> Max. :25.1558 Max. :18.1970 Max. :46.3166 Max. :22.5086
#> hot kissed dance band
#> Min. :-0.2614 Min. :-0.1958 Min. :-0.3761 Min. :-0.2958
#> 1st Qu.:-0.2614 1st Qu.:-0.1958 1st Qu.:-0.3761 1st Qu.:-0.2958
#> Median :-0.2614 Median :-0.1958 Median :-0.3761 Median :-0.2958
#> Mean : 0.0000 Mean : 0.0000 Mean : 0.0000 Mean : 0.0000
#> 3rd Qu.:-0.2614 3rd Qu.:-0.1958 3rd Qu.:-0.3761 3rd Qu.:-0.2958
#> Max. :18.5623 Max. :45.3319 Max. :18.7830 Max. :19.2610
#> marching music rock god
#> Min. :-0.1366 Min. :-0.6308 Min. :-0.339 Min. :-0.4049
#> 1st Qu.:-0.1366 1st Qu.:-0.6308 1st Qu.:-0.339 1st Qu.:-0.4049
#> Median :-0.1366 Median :-0.6308 Median :-0.339 Median :-0.4049
#> Mean : 0.0000 Mean : 0.0000 Mean : 0.000 Mean : 0.0000
#> 3rd Qu.:-0.1366 3rd Qu.: 0.1974 3rd Qu.:-0.339 3rd Qu.: 0.4508
#> Max. :33.7073 Max. :21.7306 Max. :24.272 Max. :21.8440
#> church jesus bible hair
#> Min. :-0.2773 Min. :-0.194 Min. :-0.105 Min. :-0.4028
#> 1st Qu.:-0.2773 1st Qu.:-0.194 1st Qu.:-0.105 1st Qu.:-0.4028
#> Median :-0.2773 Median :-0.194 Median :-0.105 Median :-0.4028
#> Mean : 0.0000 Mean : 0.000 Mean : 0.000 Mean : 0.0000
#> 3rd Qu.:-0.2773 3rd Qu.:-0.194 3rd Qu.:-0.105 3rd Qu.:-0.4028
#> Max. :47.2192 Max. :49.328 Max. :37.729 Max. :17.0580
#> dress blonde mall shopping
#> Min. :-0.2432 Min. :-0.1838 Min. :-0.3705 Min. :-0.4936
#> 1st Qu.:-0.2432 1st Qu.:-0.1838 1st Qu.:-0.3705 1st Qu.:-0.4936
#> Median :-0.2432 Median :-0.1838 Median :-0.3705 Median :-0.4936
#> Mean : 0.0000 Mean : 0.0000 Mean : 0.0000 Mean : 0.0000
#> 3rd Qu.:-0.2432 3rd Qu.:-0.1838 3rd Qu.:-0.3705 3rd Qu.: 0.8737
#> Max. :20.2934 Max. :39.8700 Max. :16.5196 Max. :10.4445
#> clothes hollister abercrombie die
#> Min. :-0.3166 Min. :-0.2004 Min. :-0.1825 Min. :-0.3078
#> 1st Qu.:-0.3166 1st Qu.:-0.2004 1st Qu.:-0.1825 1st Qu.:-0.3078
#> Median :-0.3166 Median :-0.2004 Median :-0.1825 Median :-0.3078
#> Mean : 0.0000 Mean : 0.0000 Mean : 0.0000 Mean : 0.0000
#> 3rd Qu.:-0.3166 3rd Qu.:-0.2004 3rd Qu.:-0.1825 3rd Qu.:-0.3078
#> Max. :16.1428 Max. :22.1627 Max. :23.7896 Max. :26.2269
#> death drunk drugs female
#> Min. :-0.2529 Min. :-0.2217 Min. :-0.1757 Min. :-2.0727
#> 1st Qu.:-0.2529 1st Qu.:-0.2217 1st Qu.:-0.1757 1st Qu.: 0.4824
#> Median :-0.2529 Median :-0.2217 Median :-0.1757 Median : 0.4824
#> Mean : 0.0000 Mean : 0.0000 Mean : 0.0000 Mean : 0.0000
#> 3rd Qu.:-0.2529 3rd Qu.:-0.2217 3rd Qu.:-0.1757 3rd Qu.: 0.4824
#> Max. :30.9186 Max. :19.6631 Max. :32.2532 Max. : 0.4824teen_clusters <- kmeans(data, k)
set.seed(2345)
#Ayer
teen_clusters <- kmeans(teens_scale, 2)
centroids<-teen_clusters$centers
class(centroids)
#> [1] "matrix" "array"
fviz_cluster(teen_clusters, data = teens_2 , stand=F)
Transforming into matrix, for making a plot. as.matrix(teen_clusters$centers)
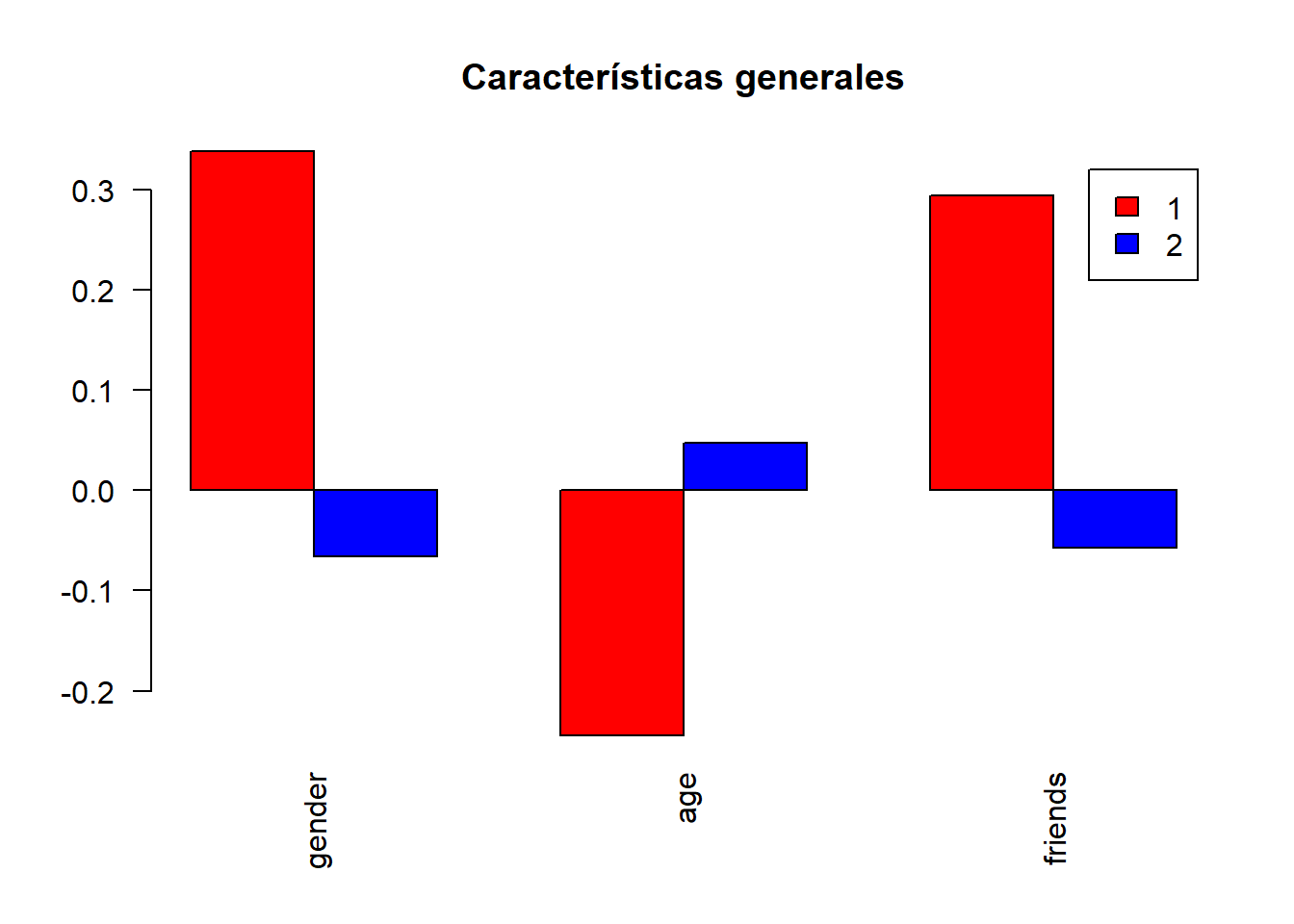
barplot(height =centroids,main="Centroids",legend.text = TRUE,
beside = TRUE,col=c("red","blue"),las=2)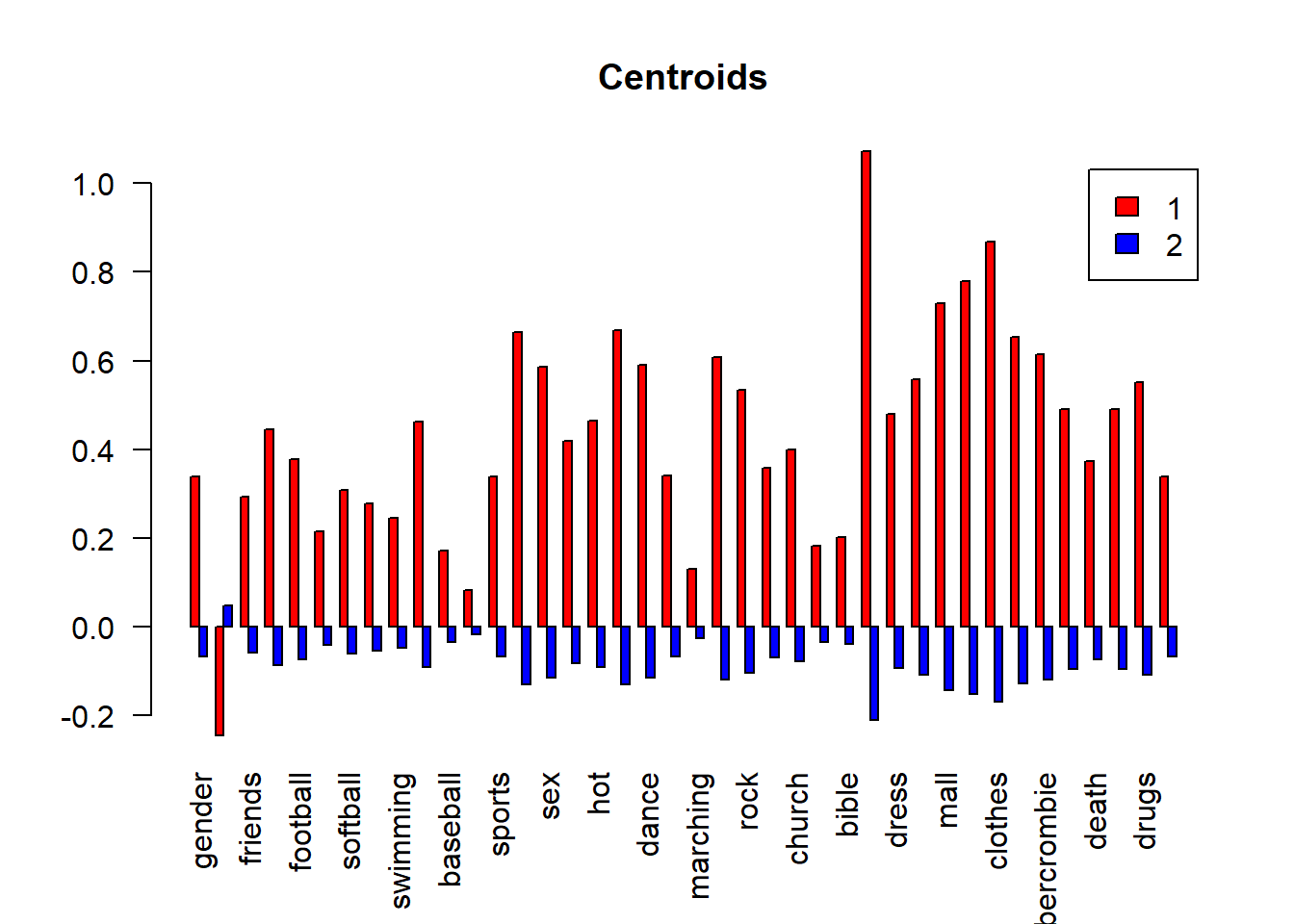
Function to make a bar plot
# data is a matrix object with the centroids
# name is the plot name (main argument)
my_plot<-function(data,name){
barplot(height =data,main=name,legend.text = TRUE,
beside = TRUE,col=c("red","blue"),las=2)}
se<-seq(1,2,1)
hc_caract<-centroids[,c("gender","age","friends")]
my_plot(hc_caract,"Características generales")